【統計学】分散と標準偏差を、できるだけていねいに解説
統計学を学ぶ際、まず最初のつまづきとして挙げられるのが「標準偏差」と「分散」。
このページでは、それらをできるだけわかりやすく解説することを心掛けています。
・動画版
【今回の目標・見取り図】
- 「分散」を感覚的、直感的に理解する
- 「分散の式の意味」を理解する
- 「分散と標準偏差の関係」を理解する
【分散とは】
分散‥‥「データのバラつき具合」を示したもの。
分散の値が大きい⇒「バラつきが大きい」もの、となります。
【たとえば・・・】
ここに「数学」と「国語」、2つのテストがあったとします。
平均点は共に70点ですが、その中身は随分と異なります。国語では個々のテスト点が平均点近辺なのがほとんどであるのに対し、数学では最高得点と最低得点の間で65点もの差があります。
| A | B | C | D | E | 平均点 | |
| 数学 | 50 | 100 | 35 | 80 | 85 | 70 |
| 国語 | 70 | 80 | 65 | 75 | 60 | 70 |
[国語と数学のテストの違い]
平均点はどちらも70点だけど…
・数学:最高100点 最低35点
・国語:最高80点 最低60点
[グラフにするとこんな感じ]
(青い棒グラフが「テストの点数」、オレンジの横線が「平均点」を示しています。)
・数学
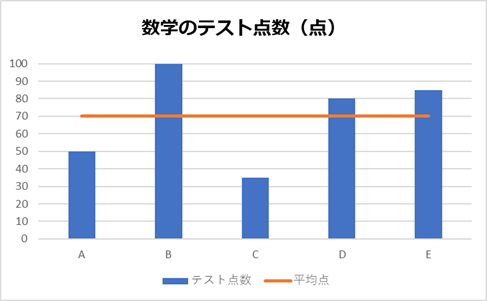
・国語
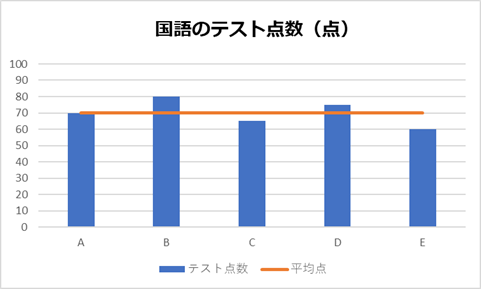
・上の2つのテスト、どうみてもバラつきが異なる
⇒明らかに数学のテストの方が、バラつきが大きい
[バラツキをキッチリと示したい]
「大きい」とか「小さい」といった感覚的なものではなく、数理的にキッチリとバラつきの大きさを示したい。
⇒ そこで生まれたのが「分散の式」となります。
・「分散」の式
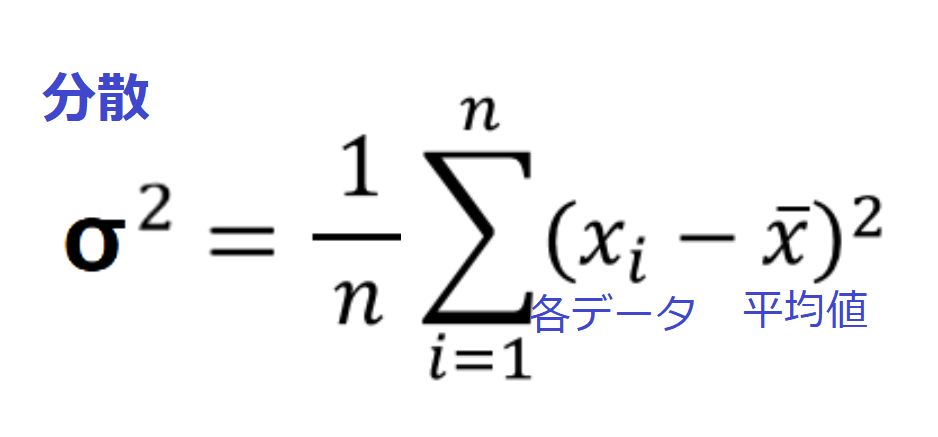
このイマイチよくわからない分散の式を、 自然言語(日本語)で表現すると次の通り。

「それぞれのデータを平均値から引いて2乗」し、そしてそれをさらに「データの数nで割る」。
実際に、さきほどの「国語」のテストで計算してみますと、
・国語のテスト
| A | B | C | D | E | 平均点 | |
| 国語 | 70 | 80 | 65 | 75 | 60 | 70 |

[分散の式の「意味」を理解する]
とはいえ、まだまだわかりにくい…。
なんで「それぞれのデータを平均値から引いて2乗」したり、「データの数nで割る」のでしょうか。
というわけで、分散を求めるための式がなぜこうなるのか、そこから考えていきましょう!
【なぜ分散では、それぞれのデータを平均値から引いて2乗するのか】
例:数学と国語のテスト結果
再び、先ほどの「数学」「国語」のテストに登場してもらいます。
・テストの点数
| A | B | C | D | E | 平均点 | |
| 数学 | 50 | 100 | 35 | 80 | 85 | 70 |
| 国語 | 70 | 80 | 65 | 75 | 60 | 70 |
【国語・数学、それぞれのテストを観察すると…】
この2つのテストのグラフ・表をじっくり観察すると、気付くことがあります。
・データのバラつきの大きい「数学」
⇒各テストの点が、平均点から離れている
・データのバラつきの小さい「国語」
⇒各テストの点が、平均点近くにまとまっている
平均点との関係に注目すると、何かがつかめそう。
というわけで、今度は「各テスト点と平均点との関係」に注目し、各テスト点数と平均点との「差」をグラフに表示してみましょう。
・データのバラつきの小さい、「国語」のテスト点数
(黄色い矢印は「テストの点数と平均点の差」)
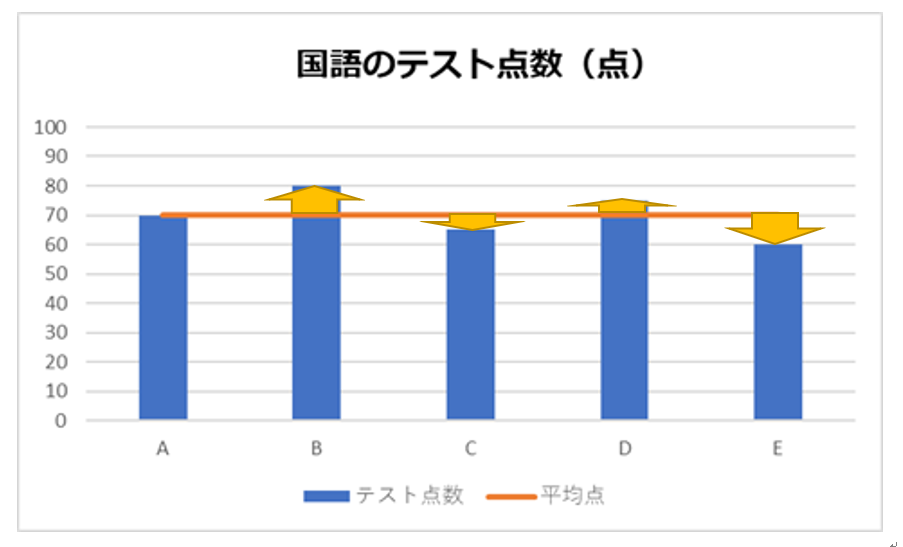
・データのバラつきの大きい、「数学」のテスト点数
(黄色い矢印は「テストの点数と平均点の差」)
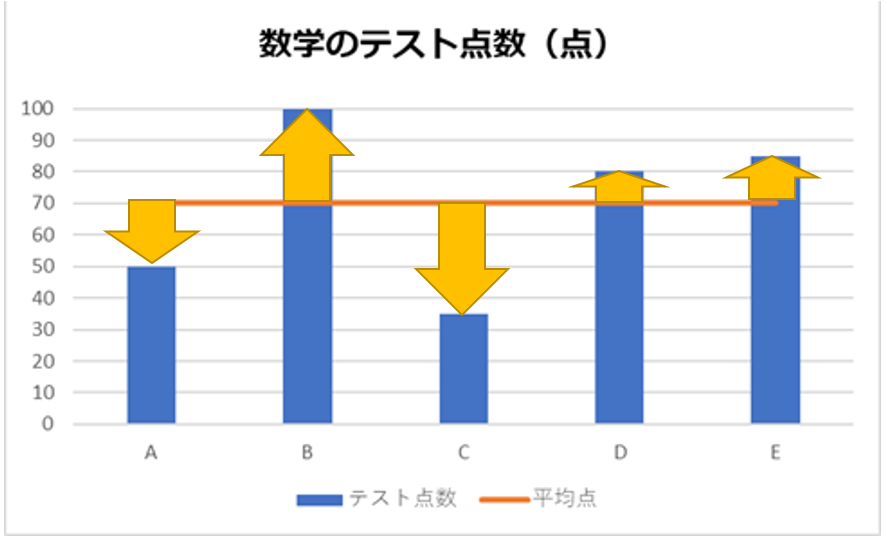
明らかに、黄色い矢印の長さが異なります。
「数学」のテストのほうが、それぞれの矢印が長い。ということは、すなわち「黄色い矢印の長さを足し合わせれば、『バラつき』を示せる」ことになります。
➾矢印の長さを足し合わすと、『バラつき』を示せる
・偏差
実は「黄色い矢印の長さ=データの値と平均値との差」のことを「偏差」といいますが、言い換えれば、この偏差を足し合わせればバラつきを示せるのです。
これが、分散の基本的な考え方となります。
先ほどの「分散の式」で示すと、赤いカッコで囲んでいる部分がコレ「偏差の足し合わせ」に当たります。
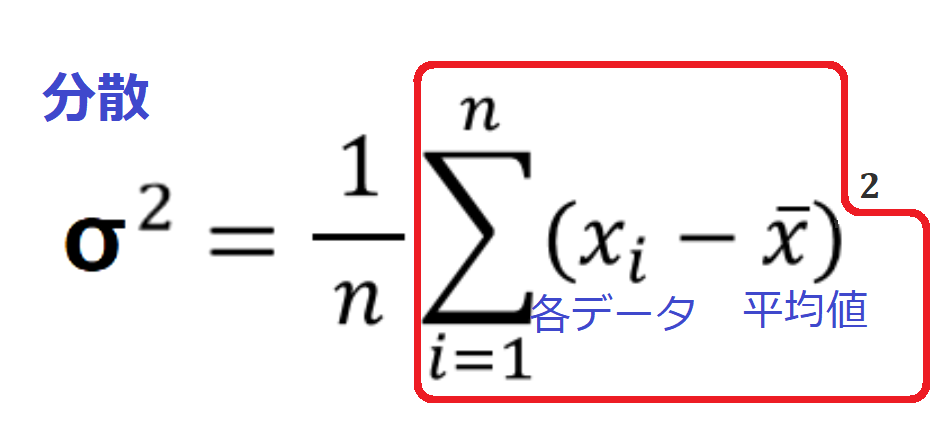
「データの値と平均との差」を2乗する意味
それにしても、まだ疑問は残ります。
バラつきを求めたいのなら、「データの値と平均との差」を足し合わせただけでも良いはず。
なぜそうせず、2乗するんでしょうか?
[実際にやってみよう]
先ほどの数学のテストにおいて、データと平均点との差を取り、それを足し合わせてみると・・・
| A | B | C | D | E | 平均点 | |
| 数学 | 50 | 100 | 35 | 80 | 85 | 70 |
| 平均点との差 | -20 | +30 | -35 | +10 | +15 | ― |
(-20)+(30)+(-35)+(10)+(15)=0
0になってしまいます。
ほかのケースでも同じ。「国語のテスト」においても、偏差を足し合わせてみると・・・
| A | B | C | D | E | 平均点 | |
| 国語 | 70 | 80 | 65 | 75 | 60 | 70 |
| 平均点との差 | 0 | +10 | -5 | 5 | -10 | ― |
(0)+(10)+(-5)+(5)+(-10)=0
やっぱり、0になってしまいます。
[偏差がだめなら、他にどんな方法があるか]
ほかには、「絶対値」を用いるという方法もあります。
すなわちマイナスの値でもプラス値でも、すべての値をプラスとして扱います。これだと、足し合わせてゼロになるということがありません。
再び「国語のテスト」で計算してみましょう。
| A | B | C | D | E | 平均点 | |
| 国語 | 70 | 80 | 65 | 75 | 60 | 70 |
| 平均点との差 | 0 | 10 | -5 | 5 | -10 |
(0)+(10)+(+5)+(5)+(+10)=30
青い箇所は、マイナスをプラスにした。
0になりません。これは一見よさそう!
ただこれだと、「計算がややこしくなる」ことに。(※高校数学で、場合分けにより絶対値の計算が面倒だったことを思い出してください)
そのため、結局は却下されます。
最終的に、
- 足して0にならないようにする
- 計算がややこしくならない
ことを満たすため、「偏差(データと平均点との差)を2乗」し、「それを足し合わせる」ことが最適となります。
さてここまで、分散の式における以下の赤井枠内の意味を説明してきました。
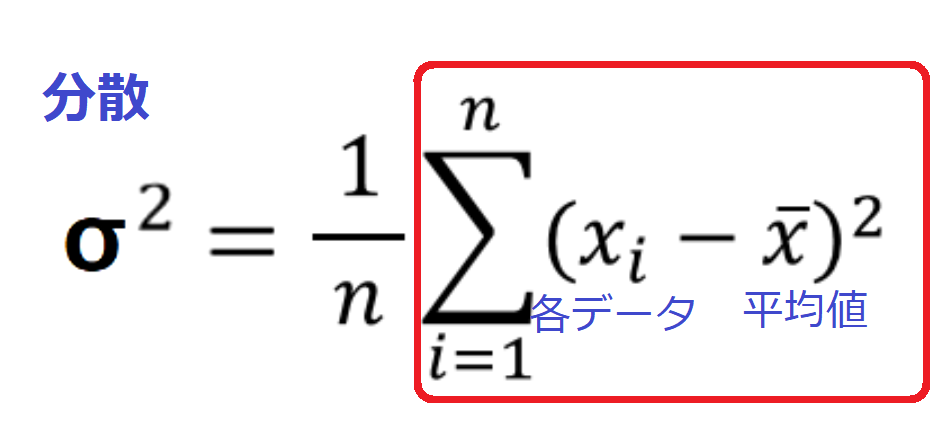
あとは最後に残っている部分、「nで割る理由」を考えます。
データの個数nで割る理由
再び分散の式の登場
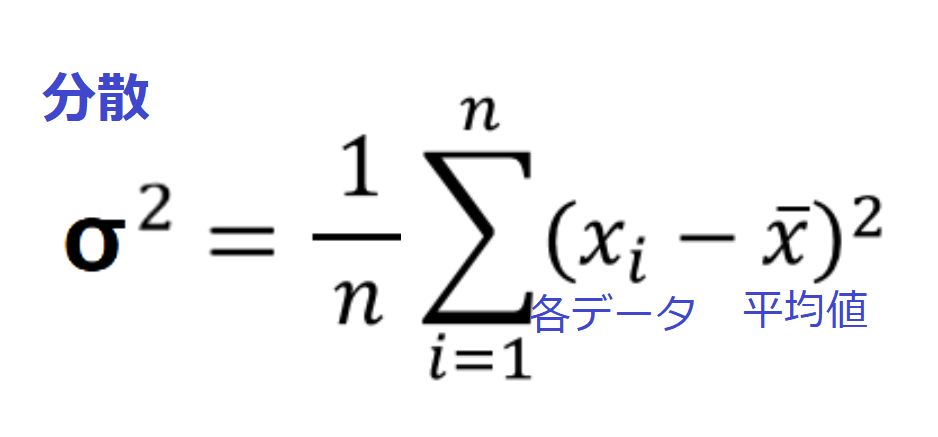
何度も言っています通り、分散は「偏差(各データを平均値から引いたもの)」を足し合わせて求めています。
しかし、このことがある「欠点」を生んでしまいます
・「欠点」とは…?
ちょっと考えてみるとわかりますが、データ数が多くなれば当然「全部足したもの」も大きくなります。
すなわち、データ数が多くなれば、実際はそれほどバラつきが大きくなくてもアウトプットも「大きい」ことになってしまいます。
・データ数関係なくバラつきを求めよう
データ数に関わらず、バラつきを求めたい。
そこで、「全部足したもの」をデータ数nで割ることにします。
【データの個数で割る意味】
またデータ数が多くなると、当然、「全部足したもの」も大きくなってしまい、バラつきが大きいということになってしまいます。
そこで「全部足したもの」をデータ数で割ることにします。そうすれば、分散がデータ数に影響されてしまうということが起こりません。
分散と標準偏差の関係
(以下、今後更新予定です)
【なぜ標準偏差が必要になるのか】
(以下、今後更新予定です)


