【統計検定対応】正規分布から確率を求める問題の解き方（統計学・確率）

【統計検定対応】正規分布から確率を求める問題の解き方（統計学・確率）

(このページは随時問題を追加していきます）

解説動画

問題1：データXがある値（A）以上になる確率

（統計検定2級でよくあるタイプの問題）

・問題

20歳~25歳の男性の身長が、平均170cm、標準偏差5cmの正規分布をすると仮定する。この時に身長180cm以上の人が抽出される確率はいくらですか？

・解き方

①：正規分布の標準化を行い、z値を求める

標準化（normalization）を行なえば、どのような平均μ（ミュー）と標準偏差σ（シグマ）をもった正規分布でも標準正規分布に変化させることができます。

問題文の場合、数値を当てはめて

となりました。

※：z値は正しくは標準化正規変数(standardized normal variable)または標準正規変数（standard normal variable)と呼ばれます。

すなわち確率

P（z≧2.0）

を求めればよいことになります。

②：標準正規分布表で読み取る（標準正規分布表の読み方）

標準化を行ない、z値⁼2.0が出ました。あとは標準正規分布表から、z値を読み取ればOK。

・標準正規分布表（上側確率）

・標準正規分布表の読み方

標準正規分布表（上側確率）とは、標準正規分布においてその値以上の値を取る確率を表しています。

実際に正規分布表を読み取る際は、「左見出しにある数値」と「上見出しにある数値」を組み合わせて読み取ります。

例えばZ⁼1.96の場合、「左見出しにある1.9」と「上見出しにある0.06」を交差させて読みことに。

すると、0.02500（2.5％）であることが分かります。

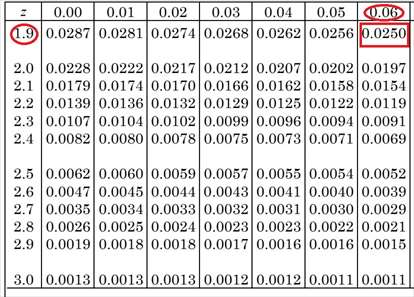
問題に戻って、Z⁼2.0を正規分布表にて読み取ると、0.0228（2.28％）。

すなわち、

P（z≧2.0）⁼0.0228

2.28％であることがわかりました。

【類題】

ある試験において、得点分布が平均58点、標準偏差10点の正規分布にしたがう場合、上位10%に入るためには、何点以上を取る必要があるでしょうか。