因果関係と相関関係の区別を可能にする「操作変数」に関するメモ
「相関関係」と「因果関係」は異なる
・例:教育年数が賃金に与える影響
例えば教育と賃金の関係を示すものとして「ミンサー方程式」が知られており、以下のような式として示すことができます。
- log Y = β0 + β1X + u
(Y=年収、X =教育年数、u=誤差項)
この式が意味するものは、「教育年数が1年増えると、年収が100×β1%上がる」というもの。
しかしながら、これはあくまでも「相関関係」を示しただけであり、教育年数が賃金へ影響を及ぼしているかの「因果関係」があるかはわかりません。以下に示すような問題があるからです。
・3つの問題
①:説明するXと説明されるYの因果関係が逆にもなる「逆の因果性」
例:
- Y = a + bX + u なのに、X = α + βY + v の関係がある
- 「警察が多いから犯罪が起きる」⇔「犯罪が多いから警察が多い」???
- 「朝食を食べると学力が上がる」⇔「学力が上がると朝食を食べる」???
- それぞれ、逆の因果関係を導き出せてしまう
②:説明するXと誤差項uとの間にも相関関係がある「欠落変数バイアス(omitted variable)」
例:
- 先ほどの、教育と収入の関係を示したミンサー関数「 log Y = β0 + β1X + u(Y=年収、X =教育年数、u=誤差項)」を考える。
- この場合、[ 年収Y ]はその会社員の[ 能力 ]にも依存しているだろうし、[ 能力 ]と[ 教育年数X ]も相関している。
- すなわち、[ 教育年数X ]と[賃金(年収) Y]は同時に決まっている(”同時に決まっている”ゆえ、「同時決定バイアス」と呼ぶ)。
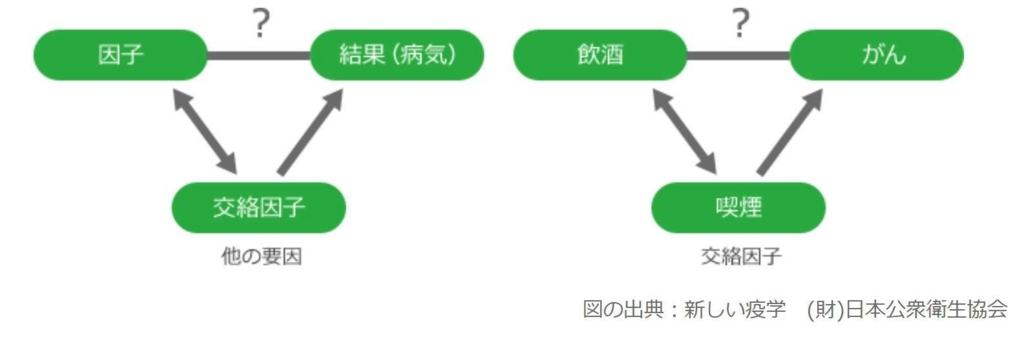
③:交絡因子(因子・説明変数X以外の因子で、現象の発生に影響を与えるもののこと)の存在
例:
- 例えば、飲酒とがんの関連性を調べようとする。この場合、がんを引き起こすとされる因子は、 [ 飲酒 ]以外にも[ 喫煙 ] などがガンの発生率に影響を与えているかもしれない。
- この場合、喫煙が交絡因子に該当する。
- その際は、喫煙が調査に影響を与えないよう、データを補正する必要がある。

これら①~③の問題は、相互作用が複雑に起こる社会現象、例えば病気や政治や経済、環境問題などでは頻繁に起こることであり、いかに適切に対処するかが課題となってきます。
因果関係を推定する「操作変数法」
これらの問題に対処するため、考案された統計的手法が「操作変数法」です。
操作変数法として最も良く知られている推定法としては、「二段階最小二乗法(Two Stage Least Squares, 2SLS)」があげられます。