人気YouTuberの再生回数と登録者の関係、ジャンルの傾向等を統計解析

YouTuberを分析してみる

売れているユーチューバーの再生回数と登録チャンネル数、ジャンルなどを参考にして、統計解析してみることにしました。

具体的にはユーチューバーのチャンネル登録者数、再生回数をデータ化しているサイト「YouTubeランキング」を元にして、上位200チャンネルほどを対象に線形回帰分析を行っています。

まずは再生回数と登録者数の関係を、Rでプロットしたものがコチラ。

・再生回数とチャンネル登録者の線形回帰

・線形回帰の出力

さて、データから回帰式

y ⁼ – 136049279.83752.47 + 752.47x

が得られました。

加えてxにくっ付いていている数（回帰係数と呼びます) 752.47は、「再生回数」の値が1大きいと、「チャンネル登録者」の値が平均して752.43大きくなることを示します。

またP値は2e-16 (e-16は、10の-16乗のこと) となっており、0.001%水準で有意。

決定係数は0.5551となっており、これは再生回数の増減がチャンネル登録者の変動の55.5％を説明できるということを示しています。結構大きいようですね。

すなわち、「再生回数が増えると、チャンネル登録者が増える傾向がある。そして、再生回数の影響はけっこう大きい」ことが、結論として言えます。

一方、変数の相関性を示す「ピアソンの積率相関係数」は次の通り。

p値は2.2e-16であり、5%水準で優位な相関関係、そして相関係数は0.789。強い相関となっています。

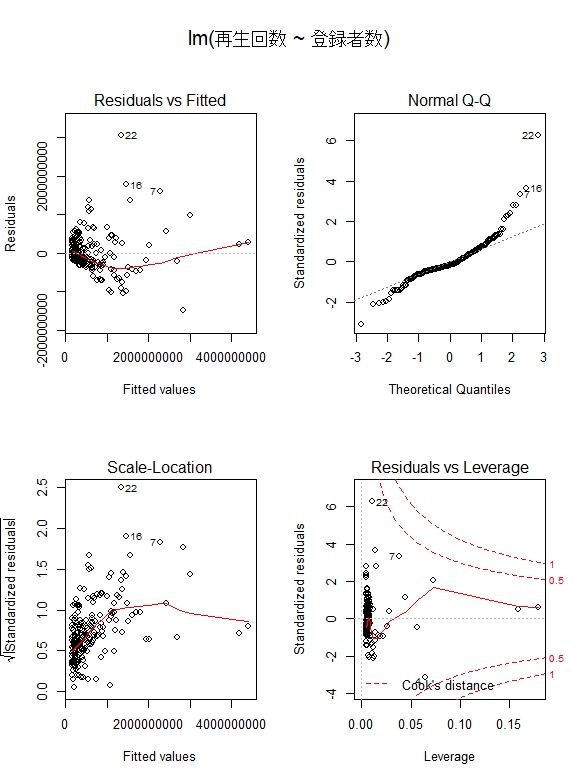
加えてこの線形回帰モデルが適切か、モデル診断を行いました。下図がその結果。

右上から時計周りに

のモデル診断図となっています。

さてモデル診断において注目したいのは、基準化残差の正規確率プロット（Normal Q-Q）。

正規確率プロットというのは、分布が正規分布になっているかを調べるもので、正規分布の際は各データが破線で示された直線上に一直線に並ぶことになります。「相関」というフレーズそのものはよく聞くところですが、しかし実は正規分布をなしていないと統計的優位にあるとは言えません。

ですが今回の場合、番号（22, 16, 7）といったデータにおいて、直線から上方に離れていることに。これは実際の残差が期待値よりも大きな値を持っていることを示すものであり、すなわち、登録者数の割に再生回数が多いことを示しています。

実はこの３つのデータって全て「キッズライン」「AAA joken TOYS」「Kan & Aki」といった、お子様向けおもちゃ紹介系動画チャンネルなんですよね。

なぜこれらトイ系・おもちゃ系動画において異様に再生回数が膨れるのか、その原理はぼんやりと想像は付くものの正確にはモチロンわからないものですが、とりあえず、この現象に注目してみたいもの。

まあ今回の話は内生性を考慮していませんし、セレクションバイアスも考慮していません。それゆえ、あくまでも「お遊び」といった感じでとらえてくださいませ。

書くのに疲れたので、取り敢えずここから先はそのうち書きます…。