相関係数の統計的有意性(意味があるか)を確認・検定する方法と、各検定の検出力の強さについて
その1:図で直感的に理解する
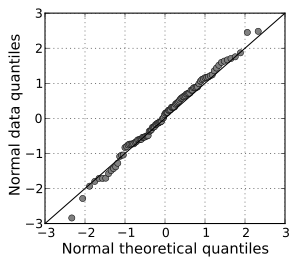
・QQプロットの例
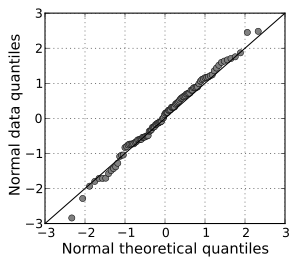
出典:Wikipedia
図で簡単に確認できる「QQプロット」。
もしプロットが一直線上に並んでいれば、観測値は正規分布に従っていることが確認でき、もし対角線から離れていれば正規分布から遠いことになります。
その2:より本格的に「正規性の検定」。コルモゴロフ・スミルノフ検定、シャピロ・ウィルク検定ほか
きちんと調べたい場合の正規性検定。
代表的なものとして、「コルモゴロフ・スミルノフ検定」「シャピロ・ウィルク検定」「アンダーソン・ダーリング検定」「リリーフォース検定(コルモゴロフ・スミルノフ検定の修正版)」といったものがあります。
ここでの帰無仮説と対立仮説は次の通り。
- 帰無仮説:母集団分布は正規分布に従う
- 対立仮説:母集団分布は正規分布に従わない
すなわち有意水準が0.05である場合、P値とその解釈は以下の通りとなります。
p値が0.05未満➾帰無仮説が棄却される➾「母集団分布は正規分布に従わない」
p値が0.05より大きい➾帰無仮説は棄却されない➾「母集団分布は正規分布に従う」
正規性検定で最も強力なのは「シャピロ・ウィルク検定」
なお2011年の研究によれば、上記検定において最も強力なのは「シャピロ・ウィルク検定」。
以下「アンダーソン・ダーリング検定」「リリフォース検定」、最後に「コルモゴロフ・スミルノフ検定」の順となっています。
シャピロ・ウィルク検定>アンダーソン・ダーリング検定>リリフォース検定>コルモゴロフ・スミルノフ検定
参考文献
Power comparisons of Shapiro-Wilk , Kolmogorov-Smirnov , Lilliefors and Anderson-Darling tests